QunaSys Tech Blog

量子コンピュータの有望な応用先として、数値流体力学（Computational Fluid Dynamics, CFD）計算が挙げられます。本技術ブログでは、QunaSysインターン上野さんを中心とした社内チームによる研究の成果について報告します。本プロジェクトでは、先行研究に対して実用化のために必要な技術開発と、QunaSysのQURI SDKを用いた量子回路実装及びシミュレーションを行いました。

CFD計算では、電磁界解析、構造解析などのその他のCAE（Computer-Aided Engineering）計算と同様に、空間をメッシュ状に区切り、各点での流速・圧力について値を保持します。シミュレーション計算では、各点の値を時間ステップを進めてアップデートしていくことで流体のシミュレーションを行います。特に旅客機など物体と流体の渦のスケール差が大きい場合など、必要なメッシュ数が大きく増大するケースも多く、乱流の近似モデルなどでメッシュ数を抑えることで対応されています。

一方で、量子計算を用いることで、指数的に格子点の多いメッシュを取り扱える可能性が期待されています。量子コンピュータではN個の数値をlog(N)個の量子ビットを用いるだけで保持することができ、たとえば40量子ビットで1兆個もの数値を保持することができます。計算時間については、最近の研究 [1] により、CFD計算においては「指数加速」と呼ばれる強い量子優位性は存在しない可能性が指摘されていますが、実用上の優位性は依然として強く期待されています。

以降本記事では、格子ボルツマン法と呼ばれる手法を用いた量子回路実装について説明していきます。まずは格子ボルツマン法について説明した後、その量子コンピュータによる計算について先行研究を紹介し、最後に弊社の研究成果について紹介します。

通常CFD計算ではナビエ・ストークス方程式と呼ばれる微分方程式を解きながらシミュレーションを行います。ナビエ・ストークス方程式は、空気や水などといった流体の運動を記述する方程式です。
ナビエ・ストークス方程式は空間の各点での流速や圧力を基本的な変数としており、流体のマクロな（分子よりもずっと大きな）スケールでの記述といえます。

しかし、実際には空気や水は分子の集合体であり、分子はニュートン力学（より正確には量子力学）に従って運動するため、よりミクロな定式化も可能です。
このアプローチを活用しながら、ナビエ・ストークス方程式と同じようにマクロなスケールでの計算を行う手法が格子ボルツマン法です。
格子ボルツマン法の出発点は、分子の集合体の運動を記述する、ボルツマン方程式です。ボルツマン方程式は分子の速度と位置に関する分布関数を変数に取り、分子の衝突と移動を記述することで、流体の運動を表現します。
ボルツマン方程式はナビエ・ストークス方程式に比べてよりミクロな記述ですが、特定の条件下では両者の等価性が成り立つことが知られています。

格子ボルツマン法では、ボルツマン方程式を格子状に区切った空間に適用し、各格子点での分布関数を計算します。定式化の過程でいくつか近似が含まれるため、主な適用先は弱圧縮と呼ばれる状態の流体のシミュレーションになりますが、その高い並列性などから、近年再度注目を集めている手法です。

量子計算においても格子ボルツマン法は、ナビエ・ストークス方程式を直接解くアプローチに比べ、陽解法による計算が可能で、各時間ステップでの操作を状態によらない固定の量子回路として効率的に実装可能な手法として期待されています。格子ボルツマン法の量子コンピュータによる計算は2021年ごろから研究が始まり[2]、文献[3]などで理論的なアルゴリズムの提案が行われました。文献[4]では、文献[3]のアルゴリズムのより具体的な実装について検討を行い、量子ビット数・量子ゲート数の見積もりを行いました。ただし、文献[4]の見積もりは量子ビット数を過大評価するなどいくつかの誤りが含まれている可能性があり、数値の解釈には注意が必要です。

文献[4]のワークフローは、球体周りの流れのシミュレーションを題材に、カーレマン線形化と呼ばれる手法で非線形効果を取り入れた、線形化された格子ボルツマン法の計算を行っています。
具体的には、量子計算は以下のようなサブルーチンの入れ子構造を持つ量子回路を実行することで実現されています。

• 空気抵抗値を計算するための量子振幅推定
• 量子振幅推定の中で複数回呼び出される、終状態計算を行うサブルーチン
• 終状態計算の中で複数回呼び出される、時間ステップ1回分の計算を行うサブルーチン

ただし、文献[4]では実際に量子回路を実装してシミュレーションを行うことはしておらず、量子ビット数・量子ゲート数の具体的な見積もりを行うにとどまっています。量子ビット数・量子ゲート数の見積もりには近似や上限値が含まれており、また非線形効果の定量的な取り扱い、流入・流出境界条件の実装など、未解決の課題も残されていました。

次節では、これらの課題に取り組む弊社の研究についてご紹介します。

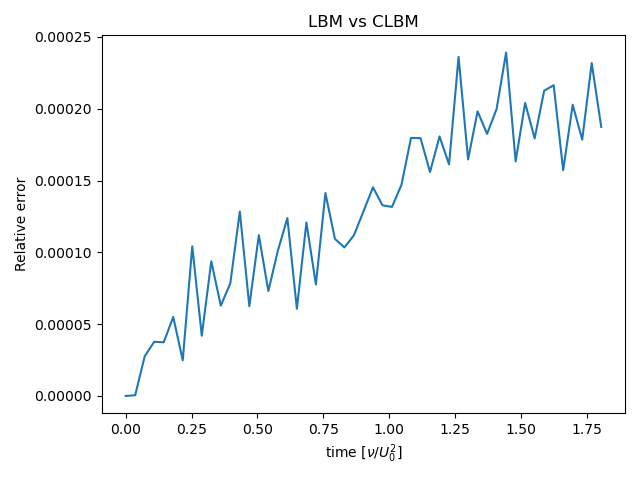
まずは線形化による非線形効果の取り込みについて、テイラー・グリーン渦を題材とした解析を行い、相対誤差がおおむねシミュレーション時間に比例することを明らかにしました。

具体的な実装に入る前に、計算量の確認のための数値解析を行いました。特に重要な値として、「条件数」と呼ばれる量があり、条件数が大きい場合は計算量も大きくなってしまいます。条件数が流体シミュレーションにおけるグリッドサイズに対してどのようにスケールするか検討を行いました。結果として、特にレイノルズ数が大きくなるほどグリッドサイズによる条件数の変化が小さいことが明らかになりました。これはレイノルズ数が大きいほどシミュレーションが困難であり、量子計算の重要性が大きくなることを考えると、有望な結果といえます。

物体周りの境界条件の処理については文献[4]ですでに取り扱われていますが、流体シミュレーションを行うためには流入・流出に関する境界条件も必要です。本プロジェクトではこれについても研究を行い、量子回路による実装を可能にしました。

いよいよ、量子回路実装を行い、（通常のコンピューター上での）量子回路シミュレーションを行います。問題設定としては16×32=512グリッドの2次元空間内に板状の物体を置いた際の流体シミュレーションを選び、線形化においてはカーレマン線形化の2次以上の寄与を無視する、すなわち非線形効果を無視する近似を行いました。

実装においてはQunaSysが開発するQURI SDKを活用しました。QURI SDKの一部であるQURI Partsのqsubというインターフェースを使うことで、今回のようなFTQCアルゴリズムの複雑な量子回路もサブルーチンを使って構造的に実装することが可能になります。qsubについての詳細はqsubチュートリアルをご参照ください。

シミュレーションにはQURI SDKを通して量子回路シミュレーションライブラリQulacsを利用しました。

今回は時間1ステップ分を量子回路実装し、時間発展を繰り返す計算を行いました。結果は以下（classical: 通常の格子ボルツマン法による計算、 quantum: 量子回路シミュレーションによる計算）のようになり、量子回路シミュレーションにより、確かに期待通りの流体シミュレーションが行えることが実証されました。

流体シミュレーションは長らく量子計算の有望な応用先とされながら、スケーラブルな量子回路実装を行い、実証を行った例はほとんどありませんでした。本プロジェクトでは、文献[3], [4]の提案を発展させ、量子回路による流体シミュレーションの実証に成功しました。

今後は、非線形効果の考慮、より複雑な問題のシミュレーション、空気抵抗など物理量の計算を含めたシミュレーションなど、量子計算による流体シミュレーションの実現に向け、研究開発を進めてまいります。

[1] K. Sakamoto and K. Fujii, "On the quantum computational complexity of classical linear dynamics with geometrically local interactions: Dequantization and universality”, arXiv:2505.10445 [quant-ph] (2025)

[2] L. Budinski, "Quantum algorithm for the Navier Stokes equations by using the streamfunction vorticity formulation and the lattice Boltzmann method", International Journal of Quantum Information 20(2) 2150039 (2022)

[3] X. Li, X. Yin, et al., "Potential quantum advantage for simulation of fluid dynamics", Phys. Rev. Res. 7, 013036 (2025)

[4] J. Penuel, A. Katabarwa, et al., “Feasibility of accelerating incompressible computational fluid dynamics simulations with fault-tolerant quantum computers”, arXiv:2406.06323 [quant-ph] (2024)